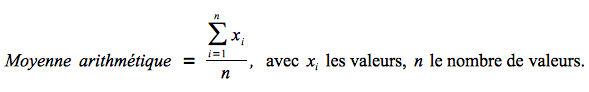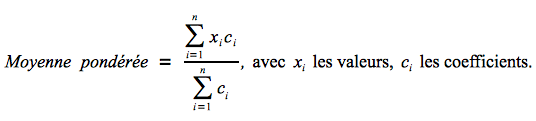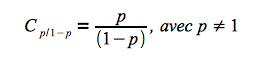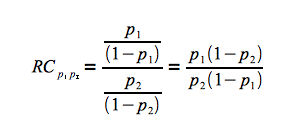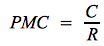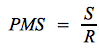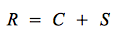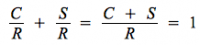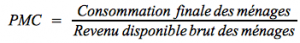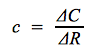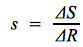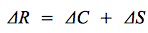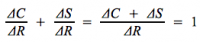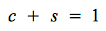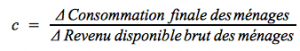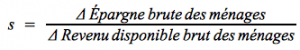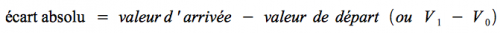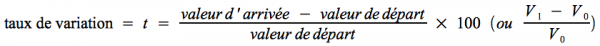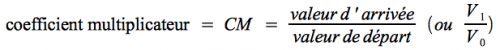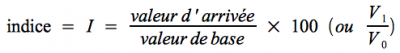Outils pour utilisateurs
Panneau latéral
Table des matières
Utiliser les outils quantitatifs
![]() Page en travaux
Page en travaux
En sciences humaines et sociales, les outils quantitatifs sont indispensables à l'analyse. Il faut donc apprendre à les manipuler.
Un peu de vocabulaire...
Un certain nombre de termes sont couramment utilisés en statistique, comme en probabilité, pour désigner les différents éléments analysés.
- Une population correspond simplement à l'ensemble des éléments étudiés.
- Un individu est un élément de la population étudiée.
Remarque : dans les deux cas, il ne s'agit pas nécessairement de personnes « humaines ».
- Un échantillon correspond à une partie des individus (un sous-ensemble) de la population étudiée.
- Un caractère correspond à une propriété (une « caractéristique », donc) possédée — ou non — par la population que l'on souhaite étudier.
- Ce caractère est dit quantitatif lorsqu'il correspond à une donnée numérique. Dans ce cas, sa valeur peut être discrète ou continue.
- Il est dit qualitatif lorsqu'il correspond à un attribut.
- Un effectif correspond à l'ensemble des individus possédant un caractère donné.
Exemple 1 :
Imaginons que l'on souhaite étudier les inégalités en France. Dans ce cas, la population correspond à l'ensemble des personnes résidant en France et un individu à une personne dans cette population.
Pour les besoins de l'étude, il est ensuite possible de ne considérer qu'une partie de cette population, l'échantillon. On peut le faire soit à l'aide d'un tirage au sort (on parle alors d'échantillon aléatoire), soit en fonction d'un ou plusieurs caractères, soit les deux. Ainsi, il serait possible de définir un échantillon de 10 000 personnes tirées au sort parmi celles résidant en Île-de-France.
Enfin, les caractères étudiés pourraient être le revenu annuel (caractère quantitatif) et la catégorie socioprofessionnelle (caractère qualitatif). Les effectifs seront donc constitués des individus possédant un certain revenu et appartenant à l'une des catégories socioprofessionnelles comme une personne bénéficiant d'un revenu de 20 000 euros annuels et appartenant aux professions intermédiaires.
Exemple 2 :
Imaginons cette fois que l'on souhaite étudier les termes d'un corpus textuel français varié (à l'image du corpus anglo-américain Brown). Dans ce cas, la population correspond à l'ensemble des termes du corpus et un individu à un terme de ce corpus.
L'échantillon pourrait correspondre à un « morceau » du corpus choisi en fonction d'un critère numérique ou du type de sources, ou les deux. Ainsi, il pourrait s'agir d'un échantillon de 100 000 mots (ou encore de 100 documents), correspondant à des textes de la presse écrite.
Enfin, les caractères étudiés pourraient être la fréquence d'occurrence des termes (caractère quantitatif) et leur domaine (caractère qualitatif). Les effectifs correspondront alors aux individus présentant une certaine fréquence d'occurrence et appartenant à un domaine donné comme les termes n'ayant qu'une seule occurrence (hapax) et appartenant au domaine de l'économie de l'environnement.
Proportions et pourcentages de répartition
La moyenne
La moyenne est une mesure de tendance centrale. C'est la valeur commune qu'aurait chaque observation de l'échantillon si toutes les observations avaient la même valeur (elle est donc un indicateur synthétique de la distribution d'une variable). La comparaison des moyennes de différents groupes de population fournit une mesure de la disparité. La moyenne arithmétique se calcule en faisant le rapport entre la somme des valeurs de l'échantillon et le nombre de valeurs de l'échantillon :
Il est également possible de calculer la moyenne pondérée en faisant le rapport entre la somme des valeurs pondérées par leurs coefficients et la somme des coefficients :
Médiane, médiale & mode
La médiane est la valeur d'une variable qui partage en deux l'effectif total de la population étudiée.
Remarque : Pour déterminer sa valeur, il faut trier les valeurs de la variable par ordre croissant.
Exemple : nombre de personnes qui perçoivent plus (ou moins) que le revenu disponible médian.
Il ne faut pas la confondre avec la médiale et le mode :
La médiale est la valeur d'une variable qui partage en deux la masse de cette variable (somme de toutes les valeurs de la variable multipliées par leurs nombres d'occurrences dans la population).
Exemple : Revenus disponibles cumulés de la population française/2. Autrement dit, la médiale est la valeur en dessous (au-dessus) de laquelle se situe 50 % du revenu disponible total de la France.
Le mode est la valeur d'une variable dont la fréquence est maximale dans la population étudiée.
Remarque : il s'agit bien d'un terme masculin.
Exemple : le revenu disponible le plus souvent constaté dans la population française.
Prenons un exemple simple pour mieux comprendre. Imaginons la distribution du revenu disponible suivante sur une population fictive de 15 personnes :
| Population | Jaja | Gigi | Fafa | Lulu | Bibi | Toto | Lili | Mimi | Dédé | Nono | Lala | Dudu | Kiki | Momo | Nana | Total |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| No | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 15 |
| Revenu disponible mensuel en euros | 1 000 | 1 000 | 1 200 | 1 400 | 1 500 | 1 500 | 1 500 | 1 700 | 1 900 | 2 000 | 2 300 | 2 400 | 2 400 | 3 100 | 5 100 | 30 000 |
Effectuons les différents calculs :
L'effectif étant de 15 personnes, la valeur médiane correspond à celle de la 8e personne, c'est-à-dire de Mimi. La médiane est donc de 1 700 euros.
Remarque : Si l'effectif était de 14 personnes (on enlève Nana, par exemple), donc pair, la médiane se situerai entre Lili et Mimi, on choisirait alors généralement le milieu de l'intervalle entre les deux, c'est-à-dire 1 600.
Concernant la médiale, il faut commencer par déterminer le revenu disponible cumulé. Ici, il figure sur la colonne Total : 30 000 euros. On peut alors facilement calculer la médiale : 30 000 euros/2 = 15 000 euros.
La médiale étant de 15 000 euros, il sera alors intéressant de constater qu'un peu plus des 2/3 de la population se partagent cette somme (le revenu disponible des 10 premières personnes est égal à 14 700 euros).
Enfin, la valeur du mode est de 1 500 euros qui présente trois occurrences dans la population (aucune autre valeur du revenu disponible n'a une fréquence supérieure ou égale à trois).
Odds ratio ou rapport de cotes
À l'origine étaient les odds...
Un odds, ou cote 1), correspond au rapport de deux évènements complémentaires au sens probabiliste. Autrement dit, si l'évènement P se réalise, non-P ne se réalise pas.
Le résultat de ce rapport montre donc la cote d'un évènement au regard de l'évènement contraire.
On effectue :
p = 1, correspondant à une division par zéro, est exclu, d'autant qu'équivalent à la certitude, cela n'a pas de sens d'effectuer ce calcul.
Interprétation des résultats :
- si C = 1, p a les mêmes chances de se réaliser que son contraire. Cela correspond à une situation d'équiprobabilité.
- si C > 1, p a plus de chances de se réaliser que (1-p). Plus on s'éloigne de 1, plus les chances d'obtenir p sont grandes au regard de son contraire.
- si C < 1, p a moins de chances de se réaliser que (1-p). Plus on se rapproche de zéro, plus les chances de réalisation de p sont faibles au regard de son contraire.
Calcul de l'odds ratio ou rapport de cotes
Un odds ratio, appelé aussi rapport de cotes, est le résultat d'un calcul en deux étapes : on commence par calculer deux cotes (les odds) ; on calcule ensuite le rapport de ces deux cotes.
Pour calculer un rapport de cotes (RC), on effectue :
Un exemple d'application
Pour comprendre son utilisation, prenons un exemple.
Répartition des individus et pauvreté au seuil à 60 % et à 50 % du niveau de vie médian selon la catégorie socioprofessionnelle agrégée de la personne de référence en 2004
| Seuil à 60 % | Seuil à 50 % | ||||
|---|---|---|---|---|---|
| nb d'individus | nb d'individus pauvres | taux de pauvreté | nb individus pauvres | taux de pauvreté | |
| Agriculteurs exploitants | 1 220 804 | 378 028 | 31,0 | 262 083 | 21,5 |
| Artisans, commerçants, chefs d'entreprise | 3 240 879 | 502 583 | 15,5 | 330 523 | 10,2 |
| Cadres supérieurs | 7 642 360 | 144 761 | 1,9 | 88 382 | 1,2 |
| Professions intermédiaires | 9 322 850 | 344 336 | 3,7 | 173 886 | 1,9 |
| Employés | 6 547 075 | 918 200 | 14,0 | 468 297 | 7,2 |
| Ouvriers | 13 504 801 | 2 057 825 | 15,2 | 988 502 | 7,3 |
| Retraités | 13 915 420 | 1 257 089 | 9,0 | 477 238 | 3,4 |
| Autres inactifs | 3 331 690 | 1 260 557 | 37,8 | 844 978 | 25,4 |
| Ensemble | 58 739 332 | 6 867 389 | 11,7 | 3 634 619 | 6,2 |
Répartition des individus et pauvreté au seuil à 60 % et à 50 % du niveau de vie médian selon la catégorie socioprofessionnelle agrégée de la personne de référence en 2006
| Seuil à 60 % | Seuil à 50 % | ||||
|---|---|---|---|---|---|
| effectifs en milliers | nb d'individus | nb d'individus pauvres | taux de pauvreté | nb individus pauvres | taux de pauvreté |
| Agriculteurs exploitants | 1 141 | 270 | 23,7 | 185 | 16,2 |
| Artisans, commerçants, chefs d'entreprise | 3 454 | 625 | 18,1 | 406 | 11,7 |
| Cadres supérieurs | 7 819 | 197 | 2,5 | 118 | 1,5 |
| Professions intermédiaires | 9 455 | 470 | 5,0 | 234 | 2,5 |
| Employés | 6 825 | 1 189 | 17,4 | 683 | 10,0 |
| Ouvriers | 12 884 | 2 119 | 16,4 | 967 | 7,5 |
| Retraités | 14 702 | 1 533 | 10,4 | 625 | 4,3 |
| Autres inactifs | 3 179 | 1 453 | 45,7 | 994 | 31,3 |
| Ensemble | 59 471 | 7 862 | 13,2 | 4 216 | 7,1 |
Note : La ligne du total ne correspond pas à la somme de celles relatives aux catégories. En effet pour quelques individus, la catégorie n'est pas renseignée, mais ces individus sont bien comptés dans l'ensemble.
Champ individus : individus appartenant aux ménages ordinaires en France métropolitaine dont la personne de référence n'est pas étudiante.
Champ revenu : le revenu déclaré du ménage est positif ou nul.
Source : Insee, « Enquête Revenus Fiscaux 2004 », Insee Résultats, n° 69 Société, juillet 2007 ; Insee, « Enquête Revenus fiscaux et sociaux 2006 et séries longues », Insee Résultats, n° 92 Société, avril 2009. Disponibles en ligne : http://www.insee.fr/fr/themes/detail.asp?ref_id=ir-erf2004&page=irweb/ERF2004/dd/erf2004_individu-pauvr.htm & http://www.insee.fr/fr/themes/detail.asp?ref_id=ir-erfs2006&page=irweb/erfs2006/dd/erfs2006_pauvr.htm
Intéressons-nous au seuil de pauvreté à 60 % du revenu médian et comparons les catégories des cadres supérieurs et celles des ouvriers :
[0,152/(1-0,152)]/[0,019/(1-0,019)] = [0,152/0,848]/[0,019/0,981] = 9,25
Autrement dit, les chances d'être pauvre sont 9,25 fois plus grandes pour un ouvrier que pour un cadre en 2004.
Pour aller plus loin :
Louis-André Vallet, « Sur l'origine, les bonnes raisons de l'usage, et la fécondité de l'odds ratio », Courrier des Statistiques, n°121-122, décembre 2007. Disponible en ligne : http://www.insee.fr/fr/themes/document.asp?reg_id=0&id=2154
Le strobiloïde
Les quantiles
Les quantiles sont des indicateurs de la dispersion d'un caractère statistique, c'est-à-dire de l'importance de l'écart entre les valeurs extrêmes de ce caractère2). Le principe des quantiles (on parle parfois de « fractiles ») est simple : il s'agit de découper une population en « tranches », selon un principe hiérarchique, de façon à pouvoir comparer les différentes tranches entre elles. Autrement dit, il faut classer des individus par ordre croissant de la variable étudiée, puis constituer des groupes ayant le même effectif. À partir de là, il devient possible de calculer des quantiles, c’est-à-dire les valeurs (les seuils) qui séparent deux groupes qui se succèdent (de même que la moyenne de chaque groupe).
Ainsi :
- les quartiles correspondent à un découpage par tranches de 25 %,
- les quintiles à un découpage par tranches de 20 %,
- les déciles à un découpage par tranches de 10 % (ceux que l'on utilise le plus souvent),
- les vingtiles à un découpage par tranches de 5 % (d'usage encore peu courant),
- les centiles (on trouve parfois abusivement le terme anglais de « percentiles ») à un découpage par tranches de 1 %.
Remarque : en anglais, le terme permillage (permille signifiant “pour mille”, ‰) désigne un découpage par tranches de 0,1 %. Ce terme n'a pas d'équivalent en français.
L'écart interquantile mesure la différence entre deux quantiles différents (et généralement opposés). Il est un indicateur de la dispersion : plus l'écart est élevé, plus la dispersion est forte ; plus l'écart est faible (proche de 0), plus la dispersion est faible.
Exemples :
- intervalle interquartile = Q3- Q1.
- intervalle interdécile = D9 – D1.
Le rapport interquantile désigne le rapport entre deux quantiles différents. Il est un indicateur de la dispersion : plus le rapport est élevé, plus la dispersion est forte ; plus le rapport est faible (proche de 1), plus la dispersion est faible.
Exemples :
- rapport interquartile = Q3/Q1.
- rapport interdécile = D9/D1. C'est celui que l'on utilise le plus souvent.
Pour aller plus loin :
Observatoire des inégalités, « La mesure des inégalités : qu’est-ce qu’un “décile” ? À quoi ça sert ? », Comprendre - Les questions clés. Disponible en ligne : http://www.inegalites.fr/spip.php?article703
Courbe de Lorenz et Indice de Gini
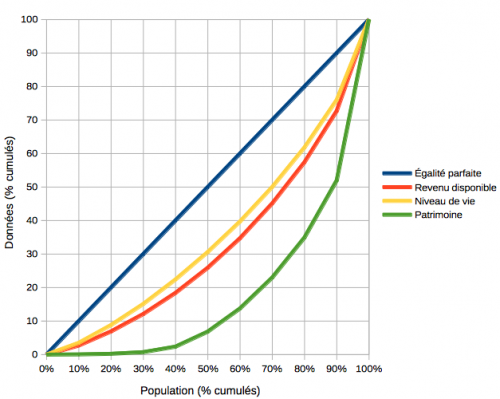
La courbe de Lorenz est une représentation graphique de la concentration d'une variable (en particulier le revenu ou le patrimoine) relativement à une répartition parfaitement égalitaire (la diagonale qui représente la répartition parfaite). Elle permet donc de représenter l'importance des inégalités en les comparant à une situation où l'égalité entre les individus (ou ménages) est strictement respectée.
Le graphique se présente sous la forme d'une boîte : à l'horizontale (axe des abscisses) on trouve la répartition de la population étudiée en pourcentage cumulés (par déciles) ; à la verticale (axe des ordonnées) on trouve le ou les indicateur(s) des inégalités étudié(s) (la ou les variables présentée(s) par déciles).
Sur le graphique est tracée la diagonale, droite qui représente une répartition parfaitement égalitaire (en bleu dans l'exemple). Est ensuite tracé, la ou les courbes de Lorenz (en jaune, rouge et vert sur le graphique), courbe(s) qui représente(nt) la répartition de la (les) variable(s) à une date donnée. Elles peuvent être distinguées par date (deux répartitions à des dates différentes pour une même population et une même variable pour visualiser l'évolution des inégalités), par population (même variable, même date, pour plusieurs populations que l'on veut comparer), par variable (même date, même population, pour montrer les effets différenciés des variables sur les inégalités), etc.
Remarque : le chiffre 50 % sur l'axe des abscisses correspond à la médiane de la population ; le chiffre 50 % sur l'axe des ordonnées correspond à la médiale.
La courbe de Lorenz permet de visualiser les inégalités en montrant l'écart entre une situation théorique d'égalité et la situation réellement constatée. Plus l'écart entre la droite de référence et la courbe est grand (la surface comprise entre la droite de référence et la courbe de Lorenz tend à occuper tout l'espace du triangle inférieur), plus les inégalités sont fortes. À l'inverse, un faible écart entre la droite et la courbe est le signe d'inégalités peu prononcées (la courbe tend à se rapprocher de la droite de référence voire à se confondre avec elle).
Document. Courbe de Lorenz
Clé de lecture : En abscisse est représentée la part des ménages en pourcentage et, en ordonnée, la part en pourcentage du revenu disponible, du niveau de vie et du patrimoine, par ordre croissant. Ainsi, sur la courbe représentant l'égalité parfaite, on peut lire que 10 % des ménages les moins riches possèdent 10 % de la richesse. Sur celle représentant le revenu disponible, 10 % des ménages les moins riches possèdent 2,7 % du revenu disponible.
Sources des données :
Enquête Revenus fiscaux et sociaux 2012 et séries longues, Insee Résultats n°164 Société, février 2015 – Distribution des revenus disponibles annuels des ménages - Masses détenues en 2012. Disponible en ligne : http://www.insee.fr/fr/ppp/bases-de-donnees/irweb/irsocerfs2012/dd/excel/irsocerfs2012_DRD02.xls
Enquête Revenus fiscaux et sociaux 2013 – Masse des niveaux de vie détenue par les x % les plus riches en 2013. Disponible en ligne : http://www.insee.fr/fr/ffc/figure/NATnon04246.xls. Autre source de données possible : DNV02.xls. Disponible en ligne : http://www.insee.fr/fr/ppp/bases-de-donnees/irweb/erfs2006/dd/excel/erfs2006_DNV02.xls
Enquête patrimoine 2010 – Masse du patrimoine détenue par les x % les plus riches en 2010. Disponible en ligne : http://www.insee.fr/fr/ffc/figure/NATnon04244.xls
C'est ici qu'intervient le coefficient de Gini. Il va permettre de mesurer précisément l'écart entre la droite de référence (la droite d'égalité parfaite) et la courbe de Lorenz.
Le coefficient de Gini est ainsi égal à s/t,
- avec s, la surface comprise entre la droite d'égalité parfaite et la courbe de Lorenz,
- et t, le triangle formé par la partie inférieure du graphique (en-dessous de la droite d'égalité parfaite).
Il est compris entre 0 et 1. Lorsqu'il est tend vers 1, la surface entre la droite de référence et la courbe est étendue. Cela signifie que toute la richesse est en possession d'un faible nombre d'individus (un seul dans le cas extrême). À l'inverse, lorsqu'il tend vers 0, la surface est faible, voire nulle. Cela signifie que la richesse est repartie de façon égalitaire (dans le cas extrême, 1 % de la population possède 1 % de la richesse).
Propension moyenne & marginale
Le concept de propension sert à mesurer l'importance d'une variable au regard de l'ensemble dans lequel elle est inclus. Cette notion occupe aujourd'hui une place centrale dans l'analyse économique des liens entre la demande et la croissance.
Son calcul correspond à celui d'une proportion, autrement dit d'un coefficient.
On distingue généralement propension moyenne et propension marginale :
- La propension moyenne correspond à la tendance observée sur l'ensemble considéré, donc pour chaque unité de cet ensemble.
- La propension marginale correspond à l'observation du résultat d'une variation d'une unité supplémentaire de l'ensemble.
C'est J. M. Keynes qui, le premier, donne toute son importance à la notion de propension en accordant une place de premier rang aux notions, complémentaires, de propension à consommer et à épargner. Ces notions sont ainsi indispensables à la compréhension du mécanisme du multiplicateur keynésien.
Il écrit :
La relation entre le revenu d'une communauté et la somme […] qu'on peut s'attendre à la voir dépenser pour la consommation dépend d'une de ses caractéristiques psychologiques que nous appellerons sa propension à consommer. En d'autres termes, tant que la propension à consommer ne varie pas, la consommation dépend du montant du revenu global, c'est-à-dire du volume de l'emploi N.
Source : John Maynard Keynes, Théorie générale de l'emploi, de l'intérêt et de la monnaie, livre I, chap. III. Version en ligne
Propension moyenne
La propension moyenne à consommer (notée le plus souvent PMC) correspond à la part de la consommation (C) dans le revenu (R). De même, la propension moyenne à épargner (PMS, “S” pour savings) correspond à la part du revenu (R) consacrée à l'épargne (S).
On a donc :
Et :
Remarque : La propension moyenne à épargner est équivalente au taux d'épargne.
Par ailleurs, le revenu d'un ménage peut faire l'objet de deux utilisations alternatives : soit il est consommé, soit il est épargné, ces deux utilisations s'excluant l'une l'autre.
Il est donc possible d'écrire :
Et donc :
Pour finir, on retient généralement les chiffres de la consommation finale des ménages et du revenu disponible brut (RDB) issus de la comptabilité nationale pour calculer la propension moyenne à consommer.
On obtient :
Concernant la propension moyenne à épargner, on retient, cette fois, les chiffres de l'épargne brute et du revenu disponible brut (RDB) pour la calculer.
On obtient :
Propension marginale
La propension marginale à consommer (notée le plus souvent c) correspond à la variation de la consommation (ΔC) lorsque le revenu varie (ΔR) d'une unité (la fameuse « dernière unité »). De même, la propension marginale à épargner (s) correspond à l'impact d'une variation d'une unité du revenu (ΔR) sur la variation de l'épargne (ΔS).
On a donc :
Et :
Il est également possible d'écrire :
Et donc :
Ou encore, en reprenant les notations plus haut :
Lorsque l'on mobilise les indicateurs de la comptabilité nationale, on obtient :
Et :
L'élasticité
Les probabilités
Les probabilités sont souvent utilisées à la suite de statistiques pour extrapoler des résultats dans un objectif de prévision. Elles sont ainsi indispensables aux sciences humaines et sociales.
Encore un peu de vocabulaire...
En probabilité, on effectue des expériences aléatoires. Comme pour les expériences de laboratoire, cela signifie que l'on cherche à réaliser différentes situations (on pourrait dire scénarios), à les tester, afin d'en observer les résultats. Ces expériences sont dites « aléatoires » car elles sont fondées sur le hasard. Un exemple souvent donné d'expérience aléatoire est le fait de lancer une pièce de monnaie ou un dé à 6 faces.
On peut réaliser ces expériences à une ou plusieurs reprises. Une réalisation particulière de cette expérience est alors appelée épreuve (il arrive cependant que les termes d'expérience et d'épreuve soient indifféremment utilisés pour désigner l'ensemble de l'expérience et ses différentes réalisations). On peut, par exemple, réaliser 10 lancers de pièce de monnaie ou dé à 6 faces, auquel cas il y a 10 épreuves de l'expérience « lancer une pièce de monnaie » ou « lancer un dé à 6 faces ».
Pour une expérience aléatoire donnée, plusieurs résultats différents sont possibles. Un événement est alors un des résultats possibles. L'ensemble des événements possibles est souvent appelé univers des [résultats] possibles ou ensemble des [résultats] possibles. Par exemple, lorsque l'on lance une pièce de monnaie, 2 événements différents sont possibles : l'événement « obtenir pile » et l'événement « obtenir face ». Lorsque l'on lance un dé à 6 faces, il y a 6 événements différents possibles : « obtenir le nombre 1 », « obtenir le nombre 2 », « obtenir le nombre 3 », « obtenir le nombre 4 », « obtenir le nombre 5 », « obtenir le nombre 6 ».
Remarque : pour caractériser les différents événements, on a le plus souvent recours aux notations utilisées dans l'étude des « ensembles » mathématiques.
Probabilités en univers fini
On parle d'univers fini (on le note généralement Ω, « oméga ») lorsque l'on connaît l'ensemble des événements possibles, c'est-à-dire l'ensemble des événements appartenant à l'univers des possibles. Dans ce cas, il est possible de définir un certain nombre d'opérations.
Si on appelle X un événement, P(X) la probabilité de réalisation de cet événement et p la valeur prise par cette probabilité, alors :
- P(X) = p
- P(X) = 1 correspond à l'événement certain.
- P(X) = 0 correspond à l'événement impossible.
Comment peut-on affirmer qu'un événement est « certain », « impossible » ou qu'il est précisément égal à p ?
L'idée repose sur la « loi des grands nombres ». Pour faire simple, il s'agit de l'idée selon laquelle lorsque l'on reproduit une expérience un grand nombre de fois, la fréquence d'apparition d'un événement (au sens statistique) tend vers sa probabilité.
Par exemple, si on lance une pièce de monnaie 3 fois, on peut très bien obtenir 3 fois « pile » (même sans tricher) et 0 fois « face ». Cependant, si on augmente le nombre de lancers, il est peu probable (le terme n'est pas anodin) que l'on continue d'obtenir « pile » à chaque lancer. On tendra plutôt à obtenir autant de fois « pile » que « face ».
Variations absolues & relatives
Variation absolue
Remarque de vocabulaire : on parle de variation absolue ou d'écart absolu.
Une variation absolue se calcule comme suit :
Autrement dit :
écart absolu = ce que je compare — ce à quoi je le compare.
L'unité dans laquelle s'exprime le résultat est celle des valeurs comparées (euros, kilos, etc.).
Cependant, lorsque l'écart absolu calculé porte sur des variables exprimées en pourcentage n'ayant pas le même ensemble de référence, leur écart absolu s'exprime en points. Voir : Outils quantitatifs :: Pourcentages et points de pourcentage
Interprétation du résultat :
— si l'écart absolu est positif alors on dira que la variable a augmenté de [résultat] unités.
— si l'écart absolu est négatif alors on dira que la variable a baissé/diminué de [résultat] unités.
— si l'écart absolu est nul alors on dira que la variable a stagné/est restée constante.
Exemples :
Si le calcul de la différence de nombre de chômeurs (quantité) entre deux dates a pour résultat 230 000, on dira : le nombre de chômeurs a augmenté de 230 000 personnes.
Si le calcul de la différence de part de chômeurs dans la population active (pourcentage) entre deux dates a pour résultat 1,2, on dira : le taux de chômage a augmenté de 1,2 points.
Variation relative
Une variation relative permet de mesurer l'importance d'une évolution. Plusieurs instruments peuvent être utilisés dans ce but : taux de variation, coefficient multiplicateur & indice.
Taux de variation
Remarque de vocabulaire : on parle de taux de variation ou de taux de croissance.
Le taux de variation s'utilise plutôt pour les variations de faible importance : en cas de baisse ou de hausse, si la variable n'a pas au moins doublé.
Le taux de variation se calcule comme suit :
Rappel : on peut se dispenser d'écrire les formules avec la mention « x 100 » dans la mesure où le signe « % » signifie, en lui-même, « sur 100 ».
L'unité dans laquelle s'exprime le résultat est le « pour cent » (%), éventuellement le « pour mille » (‰).
Interprétation du résultat :
- si le taux de variation est > 0 % alors la variable a augmenté de [résultat] %.
- si le taux de variation est < 0 % alors la variable a baissé/diminué de [résultat] %.
- si le taux de variation est = 0 % alors la variable a stagné/est restée constante.
Coefficient multiplicateur
Le coefficient multiplicateur s'utilise plutôt pour les fortes hausses. En effet, il est plus judicieux de calculer le coefficient multiplicateur lorsque la valeur a plus que doublé (si le taux de variation est supérieur à 100 %) ou perd plus de la moitié de sa valeur de départ (si le taux de variation est supérieur à - 50 %) alors qu'il vaut mieux calculer le taux de variation dans le cas contraire.
Le coefficient multiplicateur se calcule comme suit :
Il n'y a pas à proprement parler d'unité s'agissant du coefficient multiplicateur, mais le résultat s'exprime sous la forme d'un multiple de la variable de référence.
Interprétation du résultat :
- si le coefficient multiplicateur est > 1 alors la variable a augmenté, elle a été multipliée par [résultat].
- si le coefficient multiplicateur est < 1 alors la variable a diminué, elle a été divisée par [résultat].
- si le coefficient multiplicateur est = 1 alors la variable a stagné/est restée constante.
Indice
Le principal avantage de l'indice est sa facilité de lecture. De plus, il est facile de déduire de l'indice d'autres indicateurs tels le taux de variation et le coefficient.
L'indice se calcule comme suit :
L'unité dans laquelle s'exprime le résultat est point d'indice, mais cette expression est rarement utilisée. On parle plus simplement de l'indice [résultat] base [valeur de la base de référence].
Interprétation du résultat :
- si on compare à la base 100, si l'indice est > 100 alors la variable a augmenté (par rapport à la valeur de « base »).
- si on compare à la base 100, si l'indice est < 100 la variable a baissé/diminué.
- si on compare à la base 100, si l'indice est = 100 la variable a stagné/est restée constante.
Relation entre taux de variation, coefficient multiplicateur & indice
Les formules de relation entre taux de variation, coefficient multiplicateur & indice sont liées entre elles. Il est donc aisé de passer de l'une aux autres.
Ces formules sont récapitulées dans le tableau suivant :
À faire :
taux de croissance moyens
Les évolutions en volume et les évolutions en valeur
Tout d'abord, un point de vocabulaire. Les couples de termes suivants sont équivalents :
Variable « en valeur »/« en volume », « en [unité monétaire] courant(e)s » »/« en [unité monétaire] constant(e)s », « réelle »/« nominale », « non déflatée »/« déflatée ».
Ainsi on parlera indifféremment du PIB en valeur, du PIB en euros courants, du PIB nominal ou du PIB non déflaté.
Variable en volume = (variable en valeur / indice des prix) x 100
ou, ce qui revient au même :
Variable en volume = variable en valeur / coefficient multiplicateur des prix
Exemple :
Examinons la consommation sur vingt ans du ménage Machin.
| En euros | 1990 | 2000 | 2010 |
|---|---|---|---|
| Consommation finale du ménage Machin en valeur | 649,0 | 733,8 | 854,2 |
| Indice des prix à la conso base 100 en 90 | 100 | 104,4 | 112,1 |
| Coefficient multiplicateur de l’indice des prix | 1 | 1,044 | 1,121 |
| Consommation finale du ménage Machin en volume | 649,0 | 702,87 | 761,99 |
Suite à faire...
À faire :
table de mobilité table de destinée et table de recrutement
Lecture de représentations graphiques : histogrammes, diagrammes de répartition, représentations de séries chronologiques graphiques semi-logarithmiques
tableaux à double entrée, éventuellement avec subdivisions
coût marginal, productivité marginale, propension marginale (notion mathématique de dérivée)
droite des moindres carrés